Chapter 1: A President Less Remembered

James Garfield, often considered one of the less prominent U.S. presidents, has an interesting legacy. Research indicates that his name is rarely recalled when people list presidents, reflecting a certain obscurity. This is largely attributed to his presidency occurring during a relatively uneventful period in American history, situated between the Reconstruction era and the Spanish-American War. Tragically, Garfield's time in office was cut short when he was assassinated after serving just a few months, a fact that perhaps grants him slightly more recognition than his counterparts who are forgotten.

Despite this lack of notoriety, Garfield's life was rich and multifaceted. He experienced poverty during his early years and took it upon himself to learn law, eventually becoming a lawyer. His career in academia involved teaching various subjects, including mathematics, at a local college. During the Civil War, he served as a general for the Union and played significant roles in several key battles. Later, he was elected to the House of Representatives from Ohio and, after a series of terms, became president in 1880. Remarkably, he remains the only president to have been elected directly from the House.

Section 1.1: An Avid Scholar

Throughout his life, Garfield was deeply committed to self-education and was an enthusiastic reader across a wide array of subjects, mathematics included. His dedication to learning led him to develop many unique skills, one of which was his remarkable ability to write in Latin with his left hand while simultaneously writing in Greek with his right! After his congressional election, Garfield maintained his pursuit of knowledge and devised a distinctive proof of the Pythagorean Theorem—an achievement notable for its elegance. Let’s explore this proof!

Section 1.2: Understanding the Pythagorean Theorem

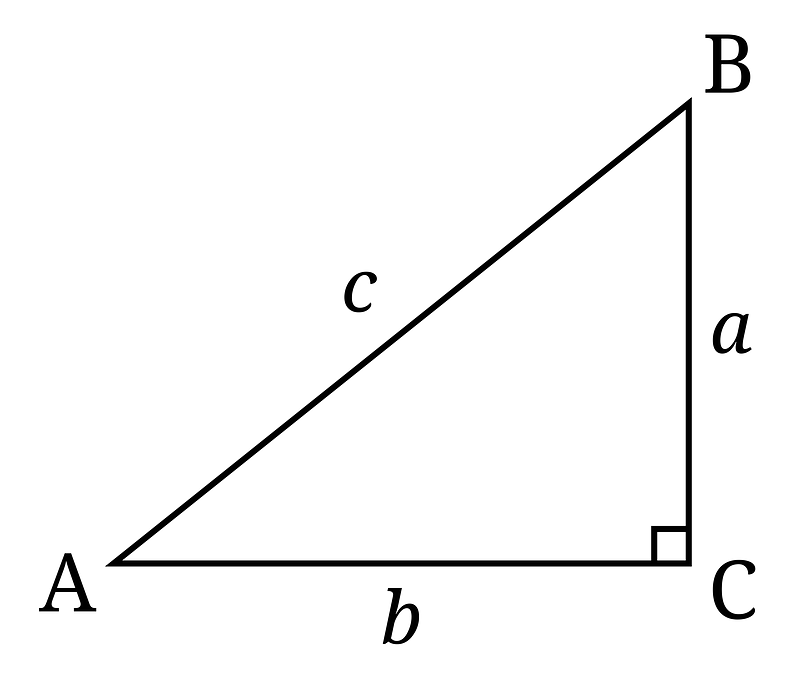
To appreciate Garfield's proof, we first need to revisit the Pythagorean Theorem, a foundational principle in mathematics that describes the relationship between the sides of a right triangle. Consider the right triangle illustrated above, where the sides are labeled a, b, and c, and angle C is defined as 90°. According to the theorem:

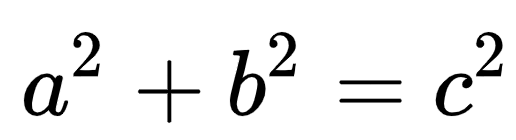
This theorem, known for over 2,000 years, has been independently discovered by various cultures, underscoring its importance in fields like architecture and engineering. One intuitive way to visualize this relationship involves area comparisons. For instance, a square with side length a has an area of a², leading us to establish further relationships.

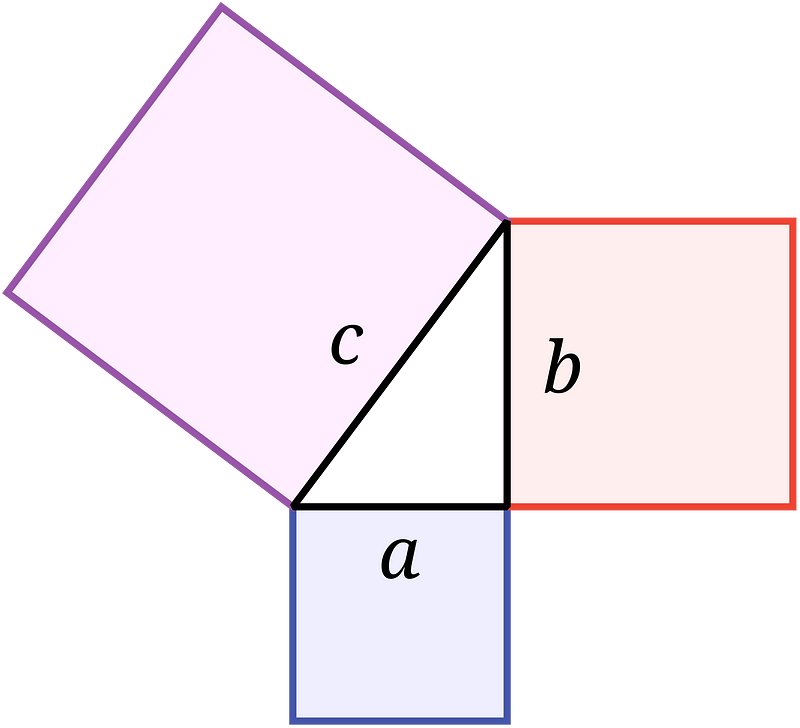
By applying the Pythagorean Theorem, we can conclude that the pink area is equivalent to the sum of the red and blue areas. Most proofs of this theorem manipulate geometric properties, and Garfield's proof is no exception.

Chapter 2: Garfield's Ingenious Proof

To understand Garfield's approach, we must re-examine the trapezoid.

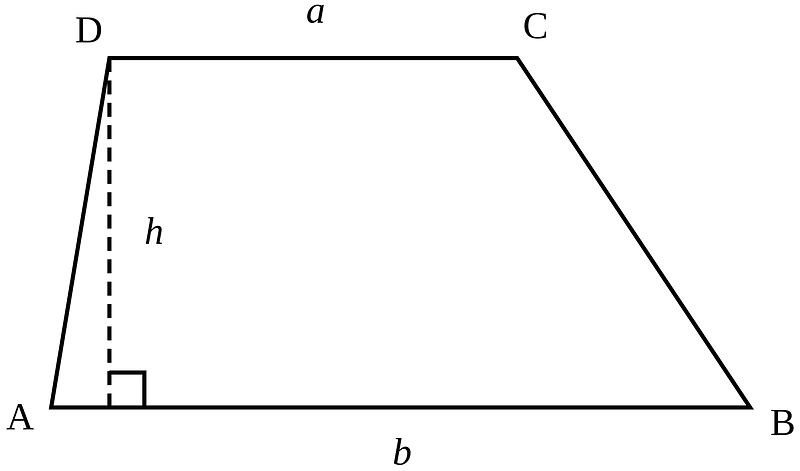
A trapezoid is defined as a four-sided figure with at least one pair of parallel sides, including squares and rectangles as special cases. The common depiction of a trapezoid can be seen above, but many variations exist.

The crucial aspect for our proof is the area formula for a trapezoid, expressed as:

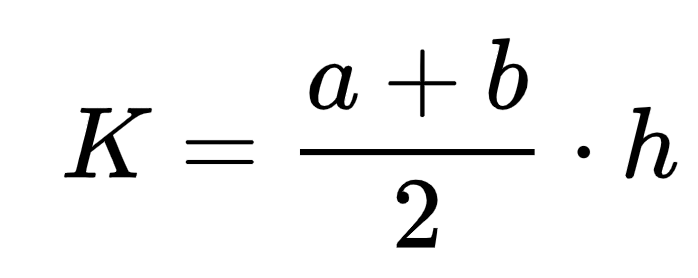
Here, a and b denote the lengths of the two parallel sides, while h represents the height. This formula can also be adapted for squares and rectangles in specific scenarios.

Garfield cleverly arranged three triangles to form a trapezoid, a configuration central to his proof.

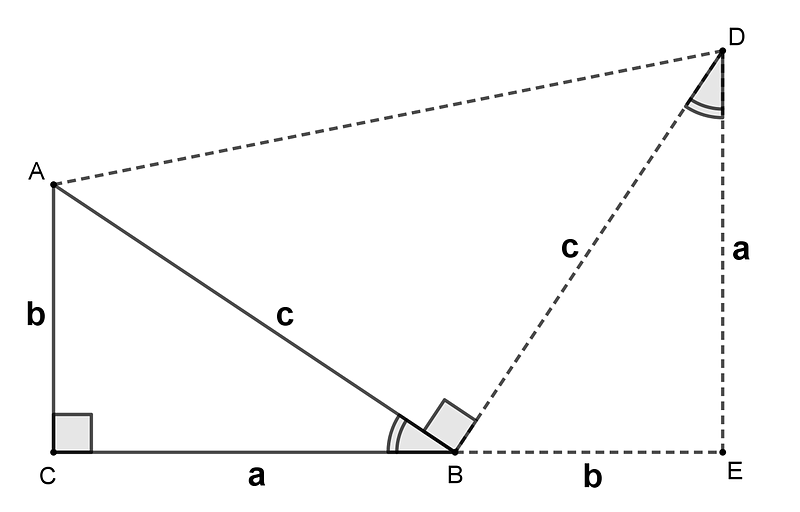
The image depicts three triangles. Notably, the two outer triangles are identical right triangles, each with dimensions a, b, and c, while the center triangle has two sides measuring c and one side of an unknown length. This arrangement leads us closer to understanding Garfield's proof.

We can confirm that the center triangle is also a right triangle based on the following relationships:

The initial relationships arise from the equivalence of the outer triangles. The subsequent relationships follow from the properties of right triangles, culminating in the conclusion that all angles in a straight line sum to 180°, confirming the middle triangle's right triangle status.

To calculate the area of this trapezoidal shape, we can apply the trapezoid area formula, yielding:

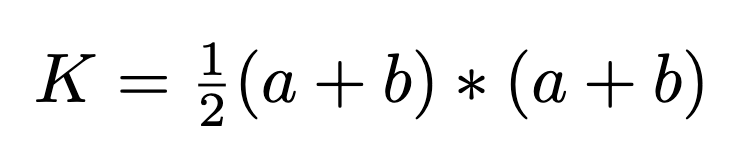
Alternatively, we can compute K by summing the areas of the three triangles, which is straightforward since they are right triangles.

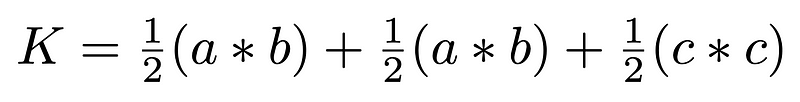
Setting these two area expressions equal leads us to the following equation:

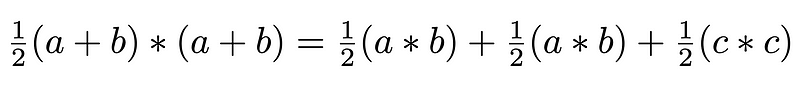
This equation can be simplified further, as outlined below.

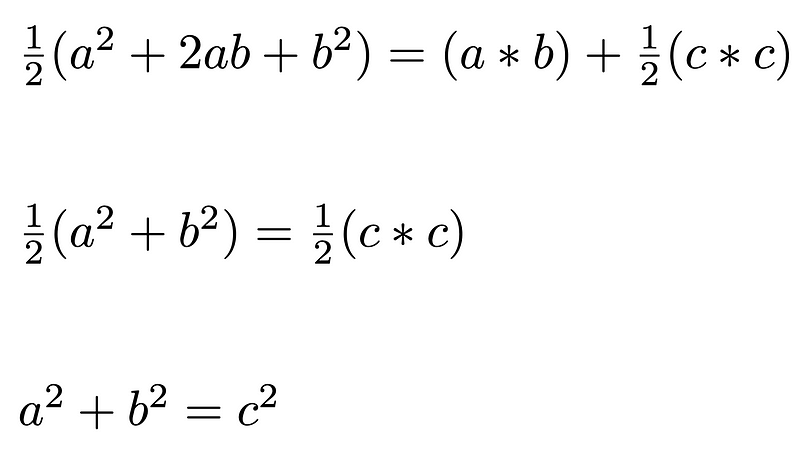
And there we have it! Through a simple geometric arrangement and a few area calculations, Garfield successfully reestablished the Pythagorean Theorem. This proof has been recognized by mathematical historians as entirely original and has inspired numerous other proofs of this iconic theorem. James Garfield’s ability to blend foundational concepts into a new proof highlights his remarkable ingenuity.

Going Further

I trust you found this exploration enlightening! James Garfield is an intriguing historical figure whose life was cut short. Had he lived longer, perhaps he would be more prominently remembered today. Fortunately, he left behind a legacy of service and this exceptional mathematical proof. For those interested in delving deeper into this topic, I've included some resources below.

If you want to learn more about Garfield's life, consider reading a well-regarded biography that covers his experiences in detail.

To explore the captivating history of the Pythagorean Theorem, check out this book—spoiler alert: Pythagoras wasn't the first to prove it!

This page on Cut The Knot features an astonishing collection of 122 different proofs for the Pythagorean Theorem, complete with explanations and visuals, making it a fantastic resource.

Also, you may find these similar articles intriguing:

• The Wild Worlds of Geometry

  Revisiting the basics can lead to all sorts of new discoveries.

  www.cantorsparadise.com

• The Unexpected Beauty of Knots

  Mathematicians find order in the most unexpected places, including knots!

  www.cantorsparadise.com

If you enjoyed this article, consider giving it a clap! You might also want to follow me for more stories or subscribe to my email list—I publish weekly on math and science topics.

A fascinating exploration of President Garfield's connection to the Pythagorean Theorem.

Discover James Garfield's unique proof of the Pythagorean Theorem in this insightful video.