Unlocking the Fibonacci Sequence: An Explicit Formula Guide
Written on
Understanding the Fibonacci Sequence
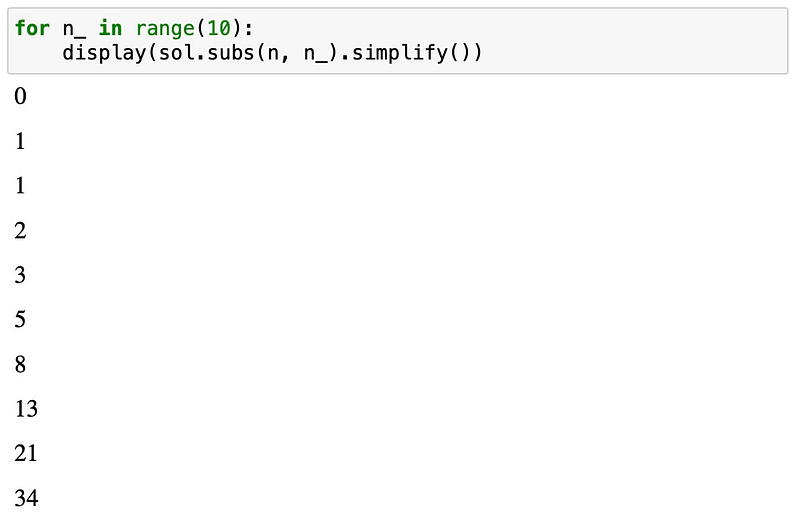
The Fibonacci sequence is a well-known series defined as 0, 1, 1, 2, 3, 5, 8, 13, 21, and so on. This sequence is typically characterized by a recurrence relation, which allows us to generate the next term based on the previous two.
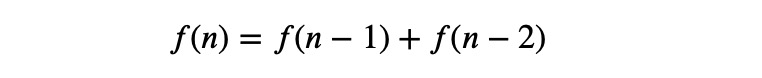
In today’s exploration, we aim to derive an explicit formula that will enable us to compute the n-th term of the sequence directly, without needing to calculate its predecessors. Our goal will be to determine F(1000).
Utilizing SymPy for Solutions
SymPy provides a powerful tool for solving recurrence equations known as rsolve. To tackle our problem, we first need to establish the necessary symbols.

The challenge lies in formatting the recurrence relation so that it equals zero, as required by rsolve. We can express it as:
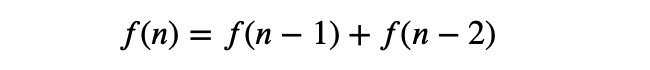
Next, we invoke rsolve:
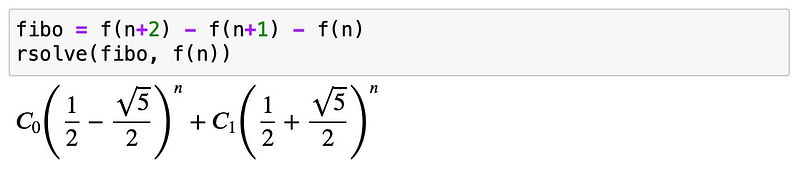
As with differential equations, establishing initial conditions is crucial for determining the constants in our solution. For the Fibonacci sequence, we set F(0)=0 and F(1)=1. These conditions are provided to rsolve in the form of a dictionary:

Exploring the Explicit Solution
The resulting explicit formula for the Fibonacci sequence is fascinating. It's well-known that this sequence relates to the golden ratio, and the explicit solution intriguingly incorporates irrational numbers. Remarkably, these irrational components combine beautifully to yield the natural numbers of the sequence.
To validate this, let’s check the initial values of the sequence:
Now, let’s compute F(1000):

It’s important to note that SymPy utilizes arbitrary precision integers, ensuring that our solution is accurate. However, the sheer size of F(1000) can make it challenging to view in its entirety without scrolling:

Fibonacci Sequence Explained
This video provides an overview of the explicit formula for the Fibonacci sequence, detailing the underlying concepts and calculations.
Delving Deeper into Recursion
In this video, we explore how to solve recursions, focusing on deriving explicit formulas for sequences like Fibonacci.