1. Recap of Two-Way ANOVA Basics

The primary objective of a two-way ANOVA is to decompose the overall variation of a dependent variable, expressed as Sums of Squares, into various sources of variation. This process helps determine if our independent variables significantly impact the dependent variable. Two-way ANOVA involves two independent variables.

There are three different approaches to dissecting variation: Type I, Type II, and Type III Sums of Squares. Notably, these methods yield different results when applied to unbalanced datasets.

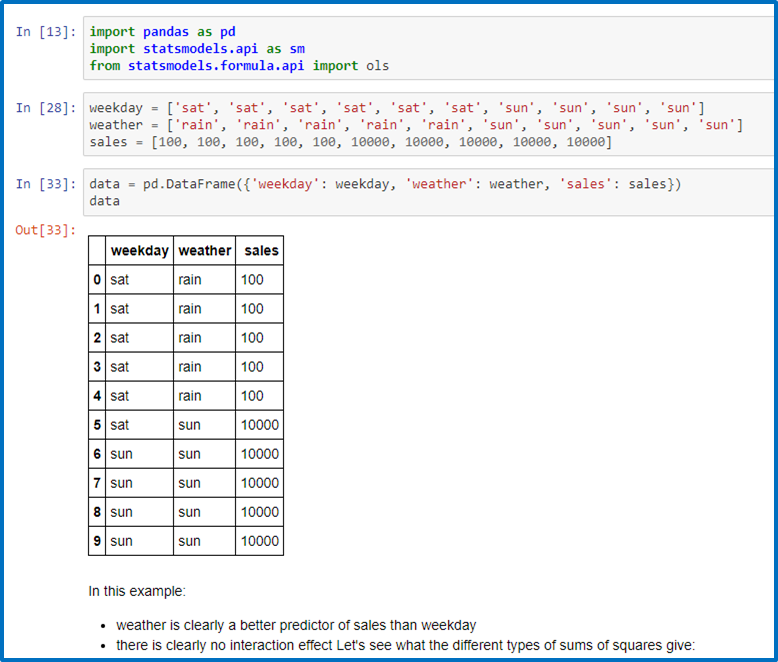
2. Type I Sums of Squares

Type I Sums of Squares, also known as Sequential Sums of Squares, allocate variation to different variables in a specified sequence. In a model with two independent variables, A and B, along with an interaction effect, the Type I Sums of Squares will:

1. Assign the maximum variation to variable A first.
2. Allocate the remaining variation to variable B.
3. Designate the interaction effect next.
4. Finally, attribute the leftover to the Residual Sums of Squares.

Due to their sequential nature, Type I Sums of Squares are sensitive to the order of variables, which is often not ideal in practical applications.

Mathematically, Sums of Squares are defined as:

• SS(A) for independent variable A
• SS(B | A) for independent variable B
• SS(AB | B, A) for the interaction effect

The conclusions drawn from Type I ANOVA indicate:

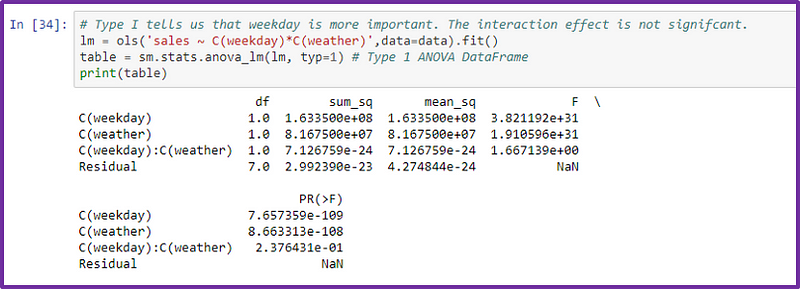
In this case, weekday was mistakenly identified as the most critical variable simply due to its order of specification.

3. Type II Sums of Squares

Type II Sums of Squares adopt a different methodology. This method accounts for the variation attributed to independent variable A while controlling for B, and vice versa. It does not consider interaction effects.

Type II Sums of Squares are best applied when there's no interaction between independent variables.

Mathematically, they are defined as:

• SS(A | B) for independent variable A
• SS(B | A) for independent variable B

The results from Type II ANOVA reveal:

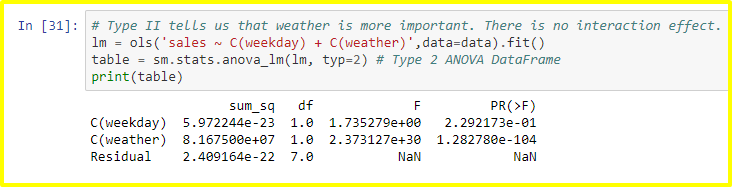
In this scenario, weather emerged as the only significant variable, which is an improvement over Type I Sums of Squares.

4. Type III Sums of Squares

Type III Sums of Squares, also referred to as partial sums of squares, provide yet another method for calculating Sums of Squares. Unlike Type II, Type III does consider interaction effects, and, similar to Type II, it is not sequential, thus the order of specification is irrelevant.

Mathematically, Type III Sums of Squares are defined as:

• SS(A | B, AB) for independent variable A
• SS(B | A, AB) for independent variable B

The results from Type III ANOVA show:

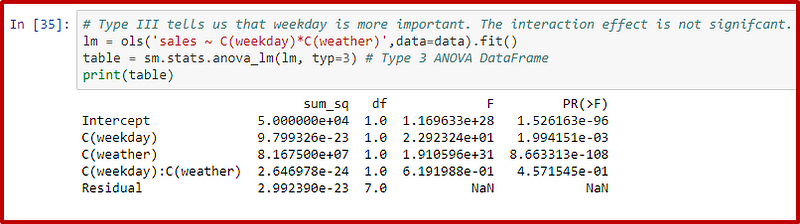
In this case, both weather and weekday are deemed significant, which is a reasonable outcome based on our example dataset.

5. Software Variability in Results

The choice of which Sums of Squares type to utilize is a subject of ongoing debate. The R programming language defaults to Type I, while Python commonly uses Type II, and SAS predominantly adopts Type III.

In R, the functions anova() and aov() implement Type I by default, but for alternative types, the Anova() function from the car package is recommended. Conversely, SAS users typically rely on Type III Sums of Squares as the default. In Python's statsmodels library, Type II is the standard, but it's easy to specify Type I or Type III as needed.

6. Conclusion: Diverse Sums of Squares for Distinct Questions

Each method for calculating Sums of Squares provides a unique perspective on how to partition shared variation. In scenarios like our example, where the correct answer is unclear, we can adopt various strategies:

• Use Type I only when there is a robust theoretical justification.
• Opt for Type II when no interaction is present.
• Choose Type III when interaction is evident.

In Type I, we prioritize the most 'important' independent variable, granting it the maximum variation. Type II disregards shared variation, assuming no interaction, which can enhance statistical power if this assumption holds true. However, should there be an interaction effect in reality, the conclusions drawn from the analysis may be misleading. Type III is preferable when interactions exist, as it seeks a balanced distribution of variation among independent variables.

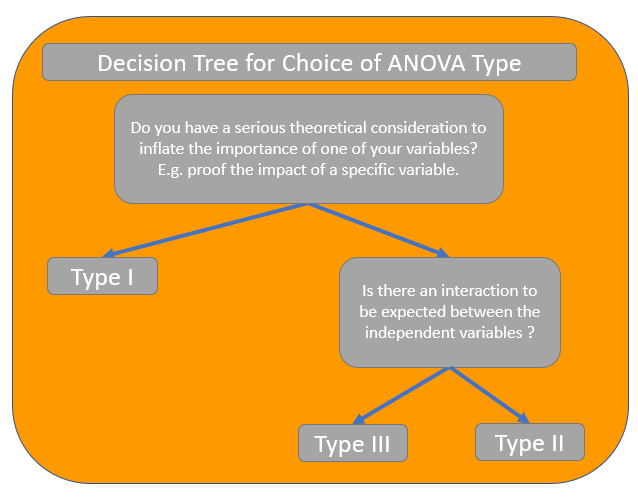
In summary, utilize Type I with caution, apply Type II when appropriate, and resort to Type III when interactions are present. I enjoyed exploring the nuances of ANOVA and hope this guide aids you in your data science journey. Thank you for reading!

This video, "The Regression Approach to ANOVA (part 2/4): Type I, II, III, IV Sum of Squares," provides further insight into the various types of Sums of Squares in ANOVA.

In this video, "Regression type I and type III sums of squares, F tests," you can explore the implications of different Sums of Squares types and F tests in regression analysis.