Chapter 1: Introduction to Orbital Motion

While a great movie doesn't necessarily need to adhere to the laws of physics, Star Trek II: The Wrath of Khan is an exemplary film, particularly for its time in 1982. Even decades later, it serves as an excellent source for physics discussions.

Let’s delve into a scene that I’ve adapted for a physics question. No need for a spoiler alert, as the movie has been out for nearly 40 years. For those unfamiliar with the plot: Captain Kirk, brimming with confidence, disregards protocol when the USS Reliant approaches without establishing communication. This oversight is critical, as the Reliant is under the control of the antagonist, Khan Noonien Singh. In a dramatic turn, Khan unleashes an attack on the USS Enterprise, leading both ships into an intense orbital chase around Regula.

With that context, we can explore the concept of orbital motion as depicted in this thrilling chase. I initially assume that both starships are in orbital motion, influenced solely by gravitational forces, much like the International Space Station orbits the Earth. However, I could be mistaken.

Here’s an illustration of the scene where both vessels are navigating around the planet.

Chapter 2: Analyzing Orbital Parameters

The display from the scene provides a wealth of information, though it's important to note that it may not represent real-time data. I can, however, make some assumptions about the accuracy of the distance scale shown in the animation, allowing me to analyze the relative speeds of the two starships.

To assess distances and velocities, I employ my preferred video analysis tool, Tracker, which is available for free. First, I need to determine the size of Regula. For simplicity, I’ll equate it to the Earth's moon, giving it a radius of approximately 1.74 million meters and a mass of around 7.35 × 10²² kilograms.

Now, let's calculate the orbital distances for both ships. Contrary to my expectations, I find I can't obtain a single value, but rather a graph depicting the distance from the center of Regula to both vessels over time.

It appears that the animation’s perspective isn’t perpendicular to the ships' trajectories, which complicates things. To simplify, I’ll calculate average distances: approximately 2.47 million meters for the Reliant and about 2.04 million meters for the Enterprise, suggesting that the Reliant is on a larger orbital path.

Now, let’s dive into some fundamental orbital physics. When an object orbits a planet or moon in a circular trajectory, the only force acting upon it is gravity. This attractive force results from the interaction between the two masses, which can be modeled using the following equation.

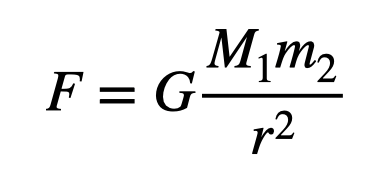
In this equation, G represents the universal gravitational constant, while r denotes the distance from the center of the planet to the object. According to Newton’s Second Law, the gravitational force causes the object to accelerate. For circular motion, the acceleration can be expressed as:

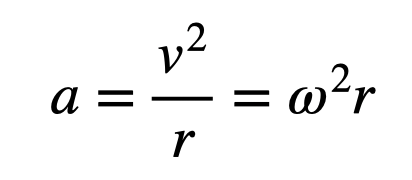
Here, ω represents the angular velocity, which is particularly relevant for our analysis of the Star Trek scenario. Setting the force equal to the mass times acceleration allows us to derive:

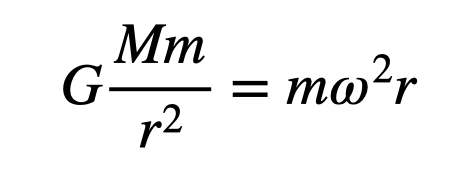
In this formulation, I've modified the mass labels to add a bit of complexity to the math. However, I can solve for angular velocity, as the mass of the orbiting object cancels out.

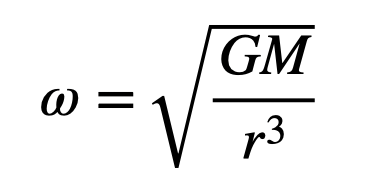
From this, it’s evident that as the orbital radius increases, the angular velocity decreases. Thus, objects in smaller orbits complete their revolutions more quickly, assuming gravitational forces are the sole influence.

Assuming Regula functions like the Earth's moon, I can compute the orbital angular velocities for both starships.

The calculations reveal that the Reliant, being farther from Regula, possesses a smaller angular velocity, indicating it won't catch up to the Enterprise based on distance alone.

But wait! What about the angular velocities derived from the animation? As previously mentioned, I lack precise timing, yet I can analyze the motion of both vessels. Here's a graphical representation of their angular positions (in radians) over time (not real time).

From the slope of this line, I can determine the angular velocity. The results show 0.27774 rad/s for the Reliant and 0.29882 rad/s for the Enterprise, yielding a ratio of 1.0759 (angular velocity of the Enterprise divided by that of the Reliant). Using the physics-based angular velocities, I calculate a ratio of 1.332, which is fairly close.

Assuming my physics calculations are correct (based on my estimations of the planet’s mass), I can use the angular velocities to determine the conversion factor between real and fictional time.

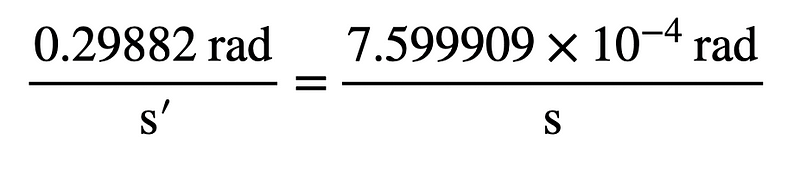
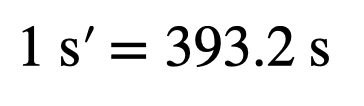
This indicates that one fictional second equals 393.2 real seconds.

Finally, I ponder a critical question: if the Enterprise is maintaining a slightly higher angular velocity, how long will it take to overtake the Reliant? With the angular data at hand, I can express their angular positions as functions of time (again, using fictional time).

By equating these angular functions and solving for time, I notice that the Enterprise starts ahead of the Reliant, leading to a negative time solution. However, if I assume the Enterprise’s angular position equals an integer multiple of 2π, they will align in space.

This leads to a calculated catch-up time of 160 fictional seconds. When multiplied by the time conversion factor of 393.2, I find that it will take approximately 17 hours for the Enterprise to catch up to the Reliant. As Spock might say: "At this pace, hours could feel like days. We will catch up to the Reliant in 17 days."

Chapter 3: The Physics Question

As a final thought, I wanted to present the physics question I devised. Here it is:

The International Space Station (ISS) orbits at an altitude of 400 km above Earth, traveling at a speed of 7670 m/s. Imagine you have another spacecraft in orbit at the same altitude but wish for it to maintain a constant speed of 10,000 m/s. To achieve this, you must activate a thruster. Given that the spacecraft has a mass of 1000 kg, what force must the thruster exert, and in which direction should it be aimed?

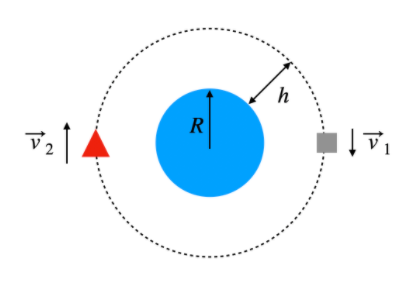
Yes, I opted for a question regarding the ISS rather than Star Trek. Additionally, here’s the answer presented in a video format.