The Quiet Transformation: How Matroid Chow Rings Are Changing Mathematics
Written on
Chapter 1: Abstract Geometric Patterns in Matroid Theory
Mathematics has evolved beyond mere calculations; it now delves into an abstract realm where constructs like matroids unveil new horizons. Matroids serve as conceptual frameworks that interconnect various elements, akin to the way atoms bond to form molecules. Their intriguing relationship with geometry and algebra creates a pathway for mathematicians to tackle problems from different angles. The idea of equivariant ?-positivity unveils a concealed symmetry within these structures. Picture this as an exquisite design that becomes visible only from a specific viewpoint. The pursuit of proving this ?-positivity for matroids transcends academic interests; it’s a discovery of patterns waiting to be utilized for addressing real-world challenges. From cryptography to network analysis, matroids promise to simplify intricate systems, revealing that order underlies apparent chaos, eager to be uncovered.
This paragraph will result in an indented block of text, typically used for quoting other text.
Section 1.1: The Symmetrical Dance of Relationships
Grasping the interconnections among various elements is a cornerstone of mathematics. Partially ordered sets (posets) present a method to articulate these connections in an almost intuitive manner. Imagine organizing a group of objects where some can coexist while others remain separate, dictated by hidden rules. When group actions are applied to posets, they introduce a layer of symmetry—akin to a mathematical ballet that aligns elements into a cohesive performance. Within the matroid framework, this symmetry is essential for comprehending their inherent properties. By scrutinizing these relationships, mathematicians have discovered fresh perspectives on longstanding problems. The elegance of this theory lies in its straightforwardness, revealing that even amidst complexity, equilibrium can be achieved, resonating through the annals of mathematics.
Subsection 1.1.1: The Power of Uniform Matroids
Uniform matroids stand out as the champions of the mathematical landscape. Their distinctive structure ensures that every subset of a specified size is equally significant, imparting a balanced and uniform character. This feature renders them invaluable tools in a variety of fields, from data analysis to quantum computing. Their apparent simplicity conceals profound depths that mathematicians are just beginning to explore. Researching the ?-expansion of these matroids resembles gazing into a cosmos of opportunities, where each equation sparkles like a star in an expansive galaxy of insights. These revelations are not merely academic milestones; they serve as foundational steps towards practical applications that could transform our approach to complex systems.
Section 1.2: Tackling the Athanasiadis Conundrum
Mathematics is rife with challenges yearning for resolution. One such enigma, introduced by Athanasiadis, tasked mathematicians with extending the ?-expansion of specific polynomials. This endeavor was not merely about numerical calculations; it aimed to deepen our comprehension of the mathematical cosmos. Recent breakthroughs in resolving this issue celebrate creativity and intellect, illuminating connections among seemingly unrelated fields. The outcome is not just a technical success; it exemplifies humanity’s capacity to unravel the mysteries of existence. It has also paved the way for new research paths and innovations, motivating future scholars to embark on their explorative journeys. The ramifications of this achievement are significant, offering fresh perspectives on the fundamental aspects of reality and encouraging us to venture beyond our current understanding.
Chapter 2: Matroids in Everyday Life
While matroids may seem abstract, they permeate our daily lives. Consider crafting a playlist; you aim for songs that fit a theme without being overly similar. Matroids ensure diversity while keeping the collection cohesive. In data networks, they optimize information flow, enabling engineers to design more effective systems. This unseen framework operates behind the scenes, facilitating complex decisions that maintain the smooth functioning of our digital existence.
The Allure of Equivariant ?-Positivity
Equivariant ?-positivity transcends mere mathematical interest; it involves uncovering latent symmetries in intricate structures. Visualize a kaleidoscope where each twist reveals a novel pattern. This is the essence of ?-positivity for mathematicians. By decoding these patterns, researchers can tackle issues in diverse fields, from computer science to biology, revealing innovative ways to model and predict complex behaviors.
Nature's Blueprint for Balance
Nature often strives for equilibrium, and uniform matroids epitomize this concept mathematically. In a uniform matroid, every element holds equal significance, fostering harmony that reflects natural processes. This characteristic renders them potent instruments for modeling systems where balance and equality are crucial. From ecological models to social networks, uniform matroids provide insights into the delicate balances that sustain life.
The Algebraic Link to Geometry
Chow rings may seem abstract, yet they form a crucial connection between algebra and geometry. They translate geometric concepts into algebraic terms, allowing mathematicians to investigate complex shapes and structures through equations. This relationship opens a myriad of possibilities, enabling researchers to deploy algebraic techniques to resolve geometric challenges, effectively bridging two seemingly distinct domains.
The Protectors of Digital Security
In our digital era, security is of utmost importance. Matroids are increasingly pivotal in cryptography, the science of secure communication. Their capacity to encode intricate relationships and ensure unique solutions makes them ideal for developing secure encryption algorithms. As our dependence on digital communication escalates, matroids will continue to serve as the guardians of our digital secrets, safeguarding our information.
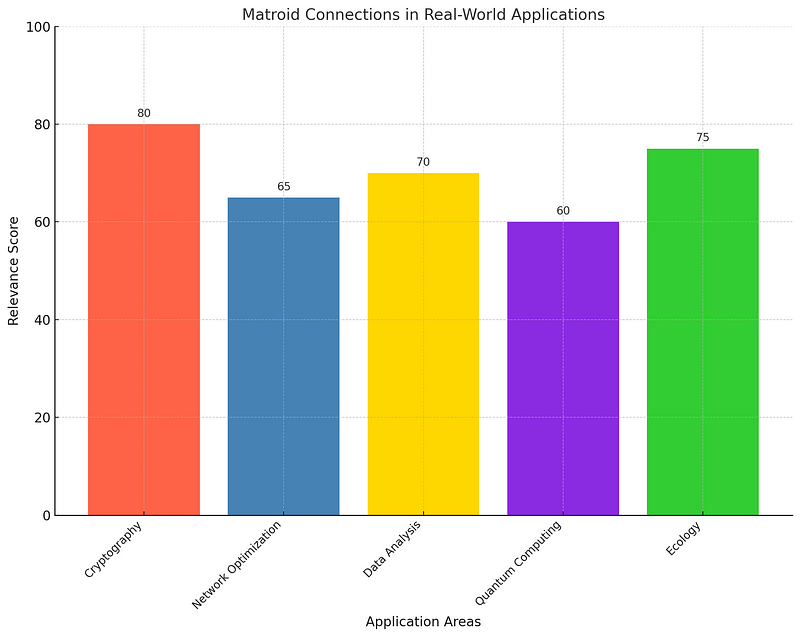
Matroid Connections in Real-World Applications
The Promise of Mathematical Advancement
Mathematics transcends being a mere subject; it represents a mindset that influences our environment. The breakthroughs in matroid theory and equivariant ?-positivity extend beyond academic pursuits. They are foundational elements for a future rich in innovation and discovery. From our comprehension of complex systems to the mechanisms of secure communication, these mathematical principles lie at the core of progress. The journey of exploration and understanding persists, inspiring us to look past the known into the realm of potential. By embracing these mathematical advancements, we can tackle challenges that once appeared insurmountable, forging a future where creativity and intellect drive transformative change.
About Disruptive Concepts
Welcome to @Disruptive Concepts — your window into the future of technology. Subscribe for fresh insights every Saturday!
Watch us on YouTube