Chapter 1: The Concept of a New Mathematical Framework

The core of my idea revolves around integrating the strengths of the Inuit vigesimal numbering system, known as Kaktovik Inupiaq, with the benefits offered by the duodecimal number system.

The Inuit method employs a base of twenty, consisting of twenty distinct symbols, and incorporates a "sub-base" made up of five components:

In this system, single units are depicted by diagonal lines that align sequentially as numbers rise (= 1, / = 2, etc.), culminating at 4 (= / /). The numeral 5 is illustrated as a single rod placed atop, which joins with other groups of five as the count progresses, reaching up to the symbol that represents 19.

For instance, the number 8 is illustrated with a top rod (5) accompanied by three lower rods ( /). Similarly, 16 is depicted as three upper rods (15) plus one lower rod. This visual approach allows for operations to be conducted in a more intuitive and graphical manner.

Addition, for example, can be visualized as a straightforward concatenation: / + / = / / (2 + 2 = 4). In cases where the addition is more complex, grouping by five simplifies the process. For instance, with 3 + 4, one can easily count up to five using the rods (marked in red), necessitating the placement of an additional rod at the top to represent five.

Adding the two remaining units (shown in blue):

Thus, the addition process is either a simple concatenation or a straightforward counting task within this numeral system.

Subtraction, conversely, involves locating the shape of the subtrahend (the second term) within the minuend (the first term) and removing it from the visual representation. For example, with 9 - 3:

The result is represented by the remaining white rods after the red ones are taken out, yielding one rod at the top and one at the bottom (6).

Basic division can be executed almost instantaneously. To find the result of 17 divided by 5, one simply counts how many times the divisor appears in the dividend (5 fits into 17 three times):

The remainder, in this case, is 2:

Longer divisions are similarly manageable. Starting from the left, we observe that the red rods fit into the dividend once, leading us to write one above:

Moving one term in the dividend reveals that the divisor appears again but in a rotated position, prompting us to write another rod and rotate it as well:

Finally, as we advance to another term, we see the divisor appears once more, allowing us to write a final rod and conclude our calculation:

Here, we’ve effectively computed 30,561 divided by 61 using a remarkably straightforward method involving visual overlays and rotations.

This method also applies to more complex divisions. In the example below, the divisor fits into the first segment of the dividend twice, hence we place two (the initial V) above:

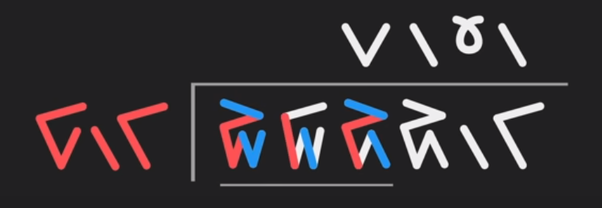
Then, it fits into the second segment once (thus another rod next to the V):

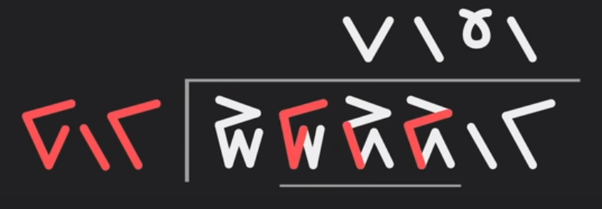
It fits zero times in the third segment:

And once in the last segment:

The outcome is what has traditionally been recorded above in the illustrations. Thus, we’ve calculated 46,349,226 divided by 2826 using simple overlays, demonstrating that long divisions can be as effortless as short ones without the need for multiplication or subtraction.

This system is both straightforward and elegant, offering a remarkable method for visualizing mathematics where operations transform into fundamental concatenations, rotations, and superimpositions of geometric shapes.

Next, let's delve into the second aspect of this exploration: the incorporation of the duodecimal system.

Chapter 2: The Duodecimal System and Its Advantages

The multiplication tables of a number system that are easiest and most consistent, are those derived from integers that divide the base of that system evenly. In this regard, 2 and 5 are notable since they are the only integers through which 10 can be divided to yield another integer.

Multiplications in a duodecimal system are more uniform because 12 can be evenly divided by more integers: 2, 3, 4, and 6. Consequently, multiplications involving these integers are just as easy to learn as the multiplication tables of 5 and 2 found in the decimal system.

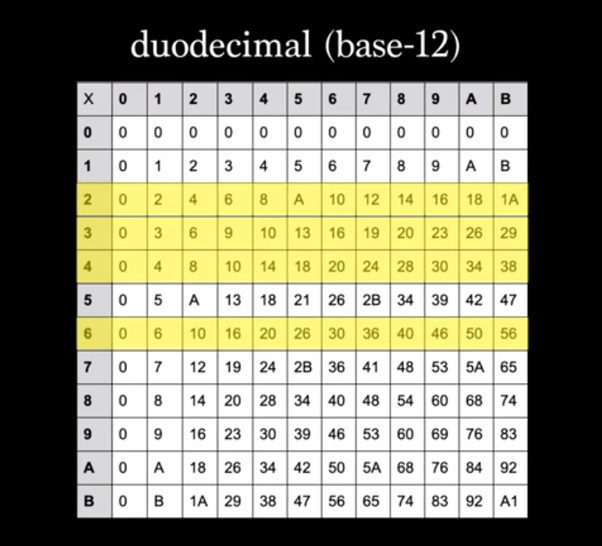
The objective I am pursuing, as previously mentioned, is to merge the visual aspects of the Inuit system with the predictable nature of duodecimal multiplication. The Inuit system retains its visual advantages even within this new base.

It appears feasible to combine the benefits of both systems by resizing the sub-base of the Inupiaq numbering. Transitioning from 20 symbols divided into four sub-bases of five elements from the original system to 12 symbols divided into three sub-bases of four elements allows for a less complex notation.

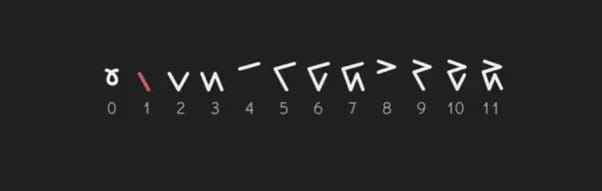
My research into alternative, more robust mathematical notations is driven by the desire to integrate these advantages. Although this is the progress made thus far, I anticipate refining the notation and enhancing this explanation in the future.

To illustrate the Inupiaq numbering system, I have referenced examples and images from this video, which serves as the source:

The first video, "A New Kind of Science - Stephen Wolfram - YouTube," highlights the innovative approaches in modern mathematics and offers insights into the visual systems discussed here.

The second video, "What We've Learned from NKS Chapter 1: The Foundations of a New Kind of Science," presents foundational concepts that align with the ideas explored in this text.