Creating a Square Wave Using Fourier Series and Python
Written on
Introduction to Periodic Waves
When it comes to generating a periodic wave—perhaps for a music synthesizer or other applications—sine or cosine waves are the simplest forms to produce. A sine wave can be obtained by considering the vertical component of a point on a circle that rotates at a constant angular speed. This is illustrated below.

Animation: Rhett Allain
The animation above was created using Glowscript; you can find the code if you're interested. However, if you're aiming to create a different periodic function, such as a square wave, it will look somewhat like this.
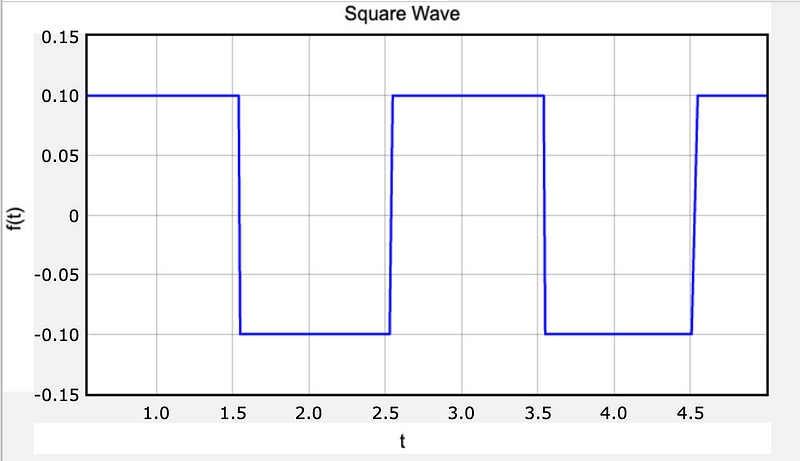
The fascinating part is that a square wave can actually be constructed using a series of sine and cosine functions. This concept forms the basis of the Fourier series.
For any periodic function ( f(t) ), it can be expressed as:
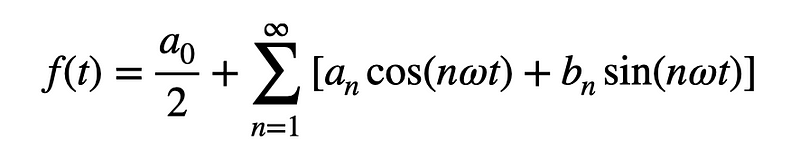
This equation represents an infinite sum of sine and cosine functions, each differing in frequency and amplitude. The frequencies are straightforward—integer multiples of ( omega ). The amplitudes can be calculated as follows:
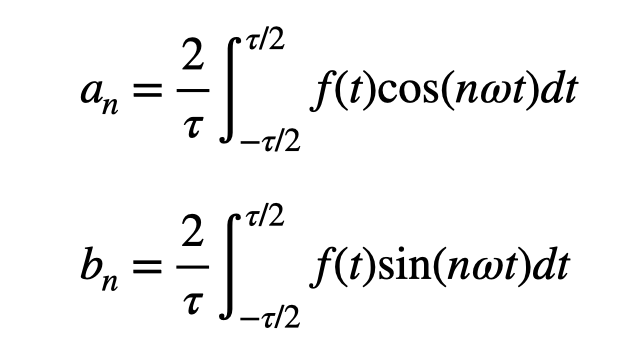
Here, ( T ) signifies the period of the periodic function, defined as:
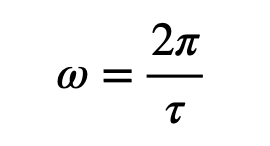
It's important to note that if the periodic function does not average to zero—meaning it does not oscillate around the t-axis—you will need to adjust it. This adjustment is represented by the term ( frac{a_0}{2} ), where ( a_0 ) is the average value over one period.
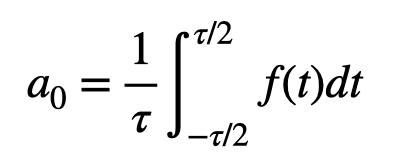
Let's proceed with constructing a model of the square wave using sine and cosine functions. While we can't add an infinite number of waves, we can certainly use around ten terms. I will demonstrate how to do this, starting with obtaining expressions for the two coefficients ( a_n ) and ( b_n ). Subsequently, I will sum the n-terms and plot the results to verify if it resembles a square wave. For this part, I will utilize Python (see my tutorial on Python plotting for reference).
Finding the Coefficients
To begin, I need a mathematical expression for the square wave ( f(t) ). Given that the function is periodic, it suffices to define it over one period.
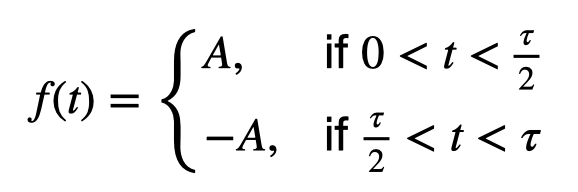
Next, I will assign values for ( A ) and ( T ).
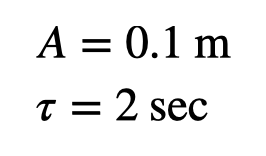
At this point, it should be evident that ( a_0 ) equals zero. Is this necessary to compute? Not really, but it’s useful nonetheless.
Let's start calculating ( a_n ) (noted with a subscript for clarity). I will integrate the function ( f(t) )—which consists of two segments—resulting in two integrals. Instead of integrating from (-frac{T}{2}) to (frac{T}{2}), I will integrate from (0) to (T).
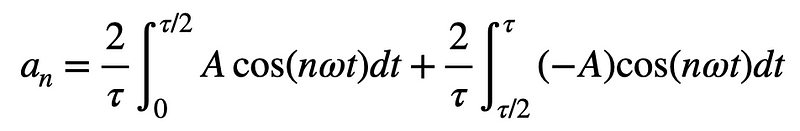
This integration is straightforward; it involves the integral of cosine.
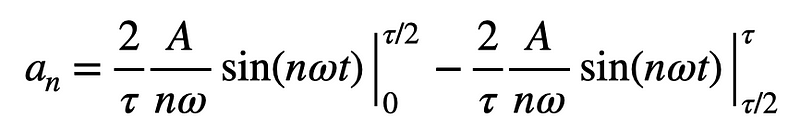
Factoring out constants and applying the limits yields:
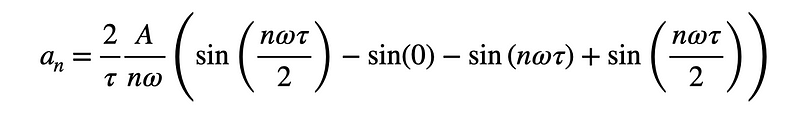
Since the sine of zero is zero, we can simplify our expression, incorporating the earlier definition of ( T ):
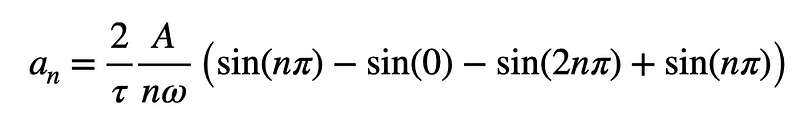
Reflecting on your trigonometry knowledge, you’ll recall that for integer ( n ), the sine of ( nomega ) will always equate to zero (as it lies on the x-axis of the unit circle). Thus, every term in this expression is zero, which may be disappointing.
This implies all ( a_n ) terms are zero. However, this is perfectly acceptable. The ( a_n ) values correspond to the coefficients for the cosine terms. Since cosine is an even function and our square wave is odd, it is logical that odd functions are used to create an odd function—therefore, cosine terms are unnecessary.
While we could have bypassed calculating the ( a_n ) terms due to the odd nature of our function, going through the process was still beneficial. It’s worth noting that not every function is strictly odd or even; some Fourier series will require both ( a_n ) and ( b_n ) terms.
Next, let’s compute ( b_n ). The procedure is similar to that of ( a_n ). I will substitute our square wave function into the definition of the ( b_n ) coefficients.
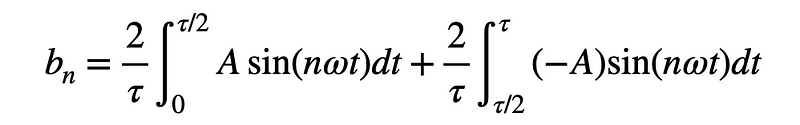
The integral of sine results in negative cosine. After integrating and applying the limits, we obtain:
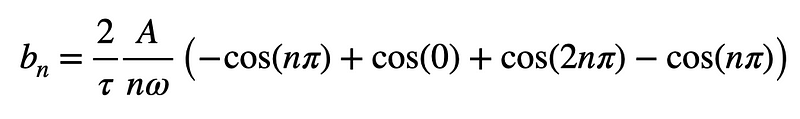
Again, the results lie on the x-axis of the unit circle (either at (0), ( pi ), or ( 2pi )—or a multiple thereof). At zero, cosine equals one, while at ( pi ), it equals negative one. Thus, the terms will either be one or negative one. Let’s simplify this expression further, as we can combine some terms and substitute for ( T ).
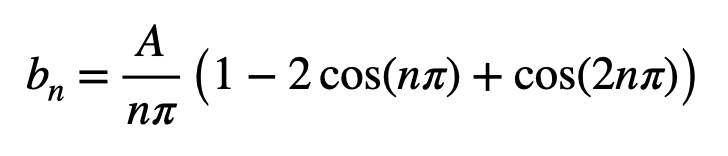
Now, let’s analyze this expression. The ( cos(2nomega) ) term always equals one, regardless of ( n ). Therefore, we have two terms that equal one. Let’s rewrite this.
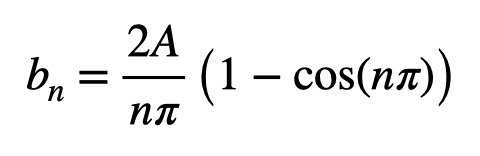
What happens when ( n = 1 )? In this case, ( cos(omega) = -1 ), making the contents of the parentheses equal to ( 1 - (-1) = 2 ). When ( n = 2 ), ( cos(2omega) = 1 ), resulting in zero. For odd ( n ), the parentheses yield two; for even ( n ), it gives zero. While you could stop here, there's a neat trick:
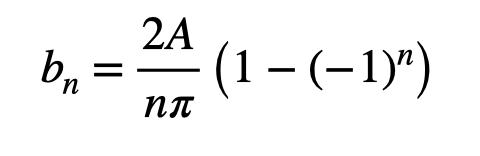
Or you could express it as:
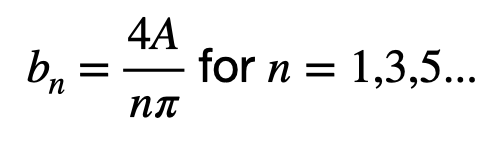
In either case, we have derived our coefficients.
Plotting the Fourier Series in Python
Now, let’s visualize the Fourier series with up to ( n = 5 ). Here is the resulting plot along with the code, which I will explain.
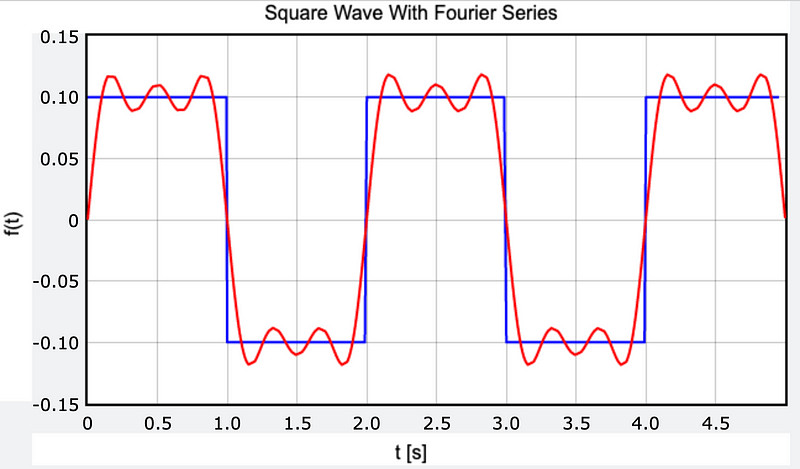
Beyond the standard graphing functions (which can be reviewed here), two key components are noteworthy. The first is a function for calculating the ( b_n ) coefficient:

What is a function in Python? Here’s a tutorial that explains it. Essentially, this function returns a numerical value for the coefficient based on a given ( n ). Yes, it is influenced by the value of ( A ), but that information is outlined above. Notice the ( (-1)^n ) term, as discussed.
How do we plot the full series? Here’s that section of the code, which I will break down for you.

Let’s discuss some specifics:
- Line 43: ( f(t) ) represents the value at a certain point. Since the Fourier series is a sum, this value starts at zero, and I can incrementally add terms.
- Line 44: ( nn ) serves as a counter variable, counting up to the maximum Fourier series (N). The "n" present is leftover from a prior attempt to implement something else.
- Line 45: This loop iterates through all values of ( n ) (1, 2, 3,…). For each ( n ) (labeled ( nn )), I simply add the Fourier term ( b_n sin(stuff) ).
- Finally, I plot that particular value for the sum of the Fourier series and repeat for the subsequent time value.
Here’s a look at the plot with ( n = 20 ) for added fun.
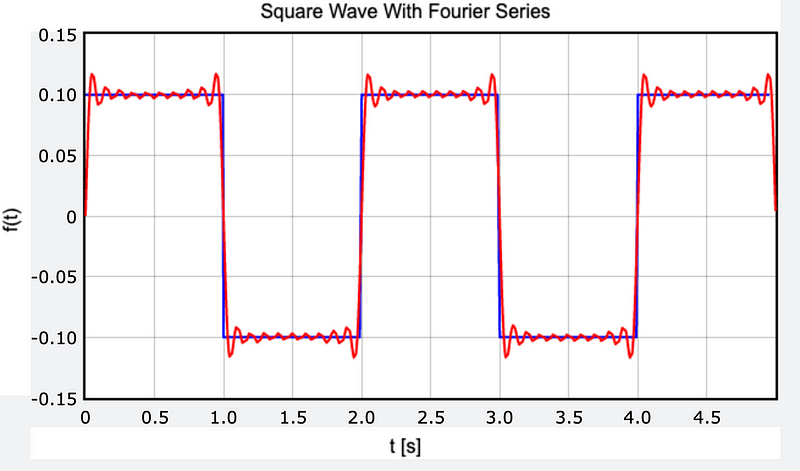
And that wraps up my work here. Next, I’m excited to explore a sawtooth wave—just for fun!
Exploring Fourier Series with Python
In the video "Fourier Series [Python]", viewers will learn how to implement Fourier series in Python, with practical examples and explanations.
The video "Fourier Series of Square Wave (Calculating Coefficients | Simulation)" demonstrates how to calculate coefficients for a square wave using Fourier series, including simulations.