The Original MAT Question and Solution

MAT 2020, Question 5

For clarity, my American audience might note that in British English, 'candy' is referred to as 'sweets.'

Let’s tackle the problem as stated. Initially, we observe that Miriam benefits from all previous sunny days during her holiday. To maximize her candy, it’s optimal for all sunny days to occur early in the holiday. Thus, if the first 15 days are sunny and the subsequent 15 days are rainy, she will gain the maximum number of sweets. Over the first 15 days, her cumulative total of sweets will equal the sum of the first 15 integers, calculated as ½ × 15 × 16 = 120 sweets. Following this, she will receive 15 sweets for each of the last 15 days, totaling 15² = 225 sweets. Therefore, Miriam’s maximum total is 120 + 225 = 345 sweets. (Her parents might be quite shocked if they did the math!)

Conversely, in the scenario where the first 15 days are rainy, she will receive no sweets, and on the final 15 sunny days, she will gain an additional sweet each day, totaling 120 sweets.

In Part (ii), if the first 15 days are sunny, Adam receives no sweets during this time. He gets 16 sweets on the 16th day, 17 on the 17th day, and so forth until he collects 30 sweets on the 30th day. Thus, Adam’s total also equals 345 sweets, identical to Miriam’s. In the situation where the first 15 days are rainy, Adam collects 1 sweet on Day 1, 2 on Day 2, up to 15 on Day 15, and then receives nothing further, yielding 120 sweets.

For Part (iii), consider a rainy day followed by a sunny one. Let k represent the number of sunny days prior to and including this rainy day. Today would contribute k sweets to Miriam’s total, while tomorrow would add k+1 sweets, resulting in a combined contribution of 2k+1 sweets. If we swap these days, today will yield k+1 sweets, and tomorrow will also yield k+1, leading to an increase of 2k+2 sweets to her total. This swapping doesn’t affect the contributions from other days, indicating that this exchange results in an additional sweet.

For Adam, on Day k being rainy followed by Day k+1 sunny, he would obtain k sweets on Day k and zero on Day k+1. By swapping them, Day k would yield zero, and Day k+1 would then yield k+1 sweets, increasing the total by one sweet as well.

In Part (iv), we are prompted to generalize our previous findings. From the first two parts, we understand that if the first 15 days are rainy followed by 15 sunny days, both Adam and Miriam consume the same number of sweets. The critical insight is that starting from this scenario, any arrangement of 15 rainy and 15 sunny days can be achieved by progressively swapping adjacent days.

If the first sunny day occurs at Day k < 16, we can modify our initial scenario by swapping Days 15 and 16. If k < 15, we continue swapping Days 14 and 15, and so on, until the first sunny day is positioned at Day k. This process can be repeated for subsequent sunny days. Notably, each swap affects Adam and Miriam's totals equivalently, allowing us to conclude that they will always end up with the same total of sweets for any holiday consisting of 15 rainy and 15 sunny days.

How about we explore this further? Have you identified a chance to generalize our earlier calculations to determine the difference in sweets consumed by Miriam and Adam, regardless of the holiday’s length or weather? Let’s revisit the problem and elevate our abstraction!

Instead of assuming a 30-day holiday with 15 rainy and 15 sunny days, let’s define the holiday as q days, with k days being rainy (k ≤ q) and q-k days being sunny.

From our prior method, we can posit that the k rainy days precede the q-k sunny days, as any arrangement can be achieved through adjacent swaps. Thus, we only need to assess the sweets difference for k rainy days followed by q-k sunny days.

For Adam, in this setup, he starts with zero sweets and gains one additional sweet each day for the first k days, after which he receives no further sweets. The total number of sweets Adam will receive can be depicted as:

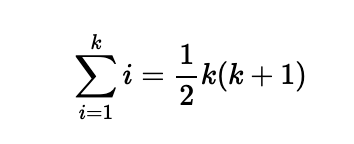
For Miriam, she receives no sweets for the first k days, followed by 1 sweet on Day k+1, and subsequently gains an extra sweet each day until Day q, resulting in:

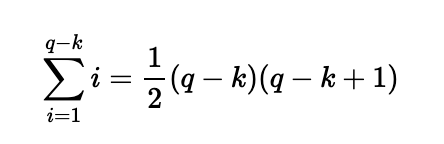
By subtracting these totals and simplifying algebraically, we can derive a general expression for the difference in sweets received by Miriam and Adam for any holiday of length q with k rainy days:

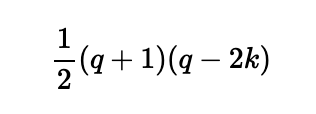
From this expression, we can immediately see that for any holiday with an equal number of rainy and sunny days (i.e., q = 2k), the difference resolves to zero, indicating that both children will receive the same number of sweets. Additionally, the result is positive when sunny days exceed rainy days (favoring Miriam) and negative when the reverse is true (favoring Adam).

What are your thoughts on this abstraction of the exam question? Please feel free to share your insights.